Entfernungsbestimmung zweier Punkte im Raum
Zur Berechnung der Entfernung zweier Punkte in einem dreidimensionalen kartesischen Koordinatensystem soll unser Dreieck aus dem vorangegangenem Beispiel dienen.
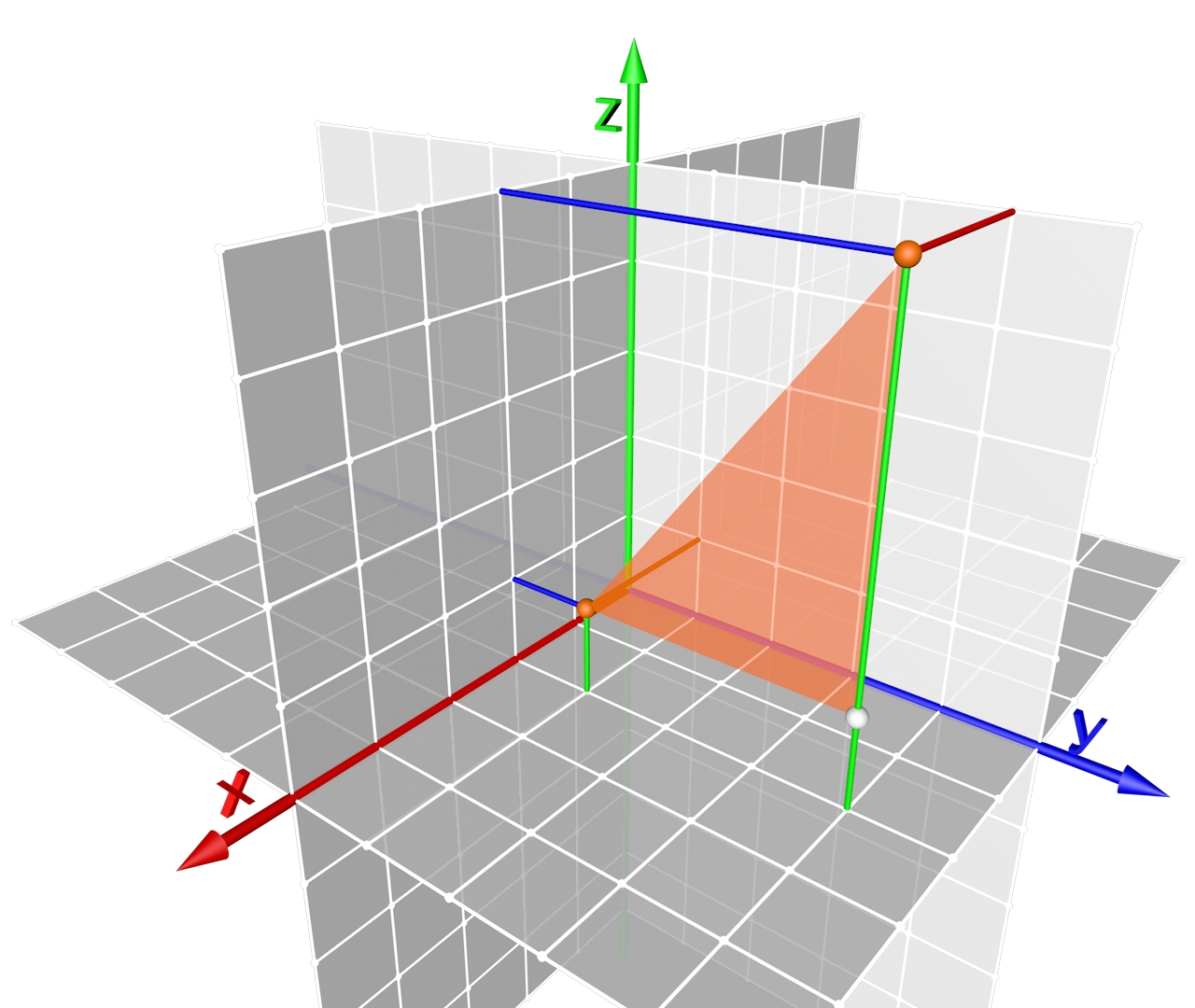
Dieses ist jetzt in einem dreidiemensionalen kartesischen Koordinatensystem aufgestellt, wie die Abbildung zeigt.
Die Hypothenuse ist die zu ermittelnde Entfernung der beiden Punkte {jmimetex}P (2,1,1){/jmimetex} (untere orange Kugel) und {jmimetex}Q (2,4,5){/jmimetex} (obere orange Kugel) unseres rechtwinkligen Dreiecks.
Die Formel zur Berechnung wird jetzt erweitert und dabei berücksichtigt, dass die Punkte jetzt über Koordinatentripel definiert sind.
{jmimetex}d = \sqrt{(P_x - Q_x)^2 + (P_y - Q_y)^2 + (P_z - Q_z)^2}{/jmimetex}
Jetzt werden wieder die Werte in die Gleichung eingesetzt.
{jmimetex}d = \sqrt{(2 - 2)^2 + (4 - 1)^2 + (5 - 1)^2} = \sqrt{0^2 + 3^2 + 4^2} = \sqrt{0 + 9 + 16} = \sqrt{25} = 5{/jmimetex}
Hinweis:
Zur einfacheren Darstellung besaßen die rechtwinklingen Dreiecke der Beispiele die Kathetenlängen 3 und 4 und die damit einhergehende Hypthenusenlänge von 5 als Sonderfall.
Im dreidimensionalen Fall müssen die Punkte des Dreiecks zudem nicht in einer Ebene liegen.
Langsam nähern wir uns der Berechnung einer GPS-Position, dazu soll jetzt zunächst gezeigt werden, wie eine Position in der Ebene bestimmt werden kann, wenn zwei bekannte Fixpunkte gegeben sind.