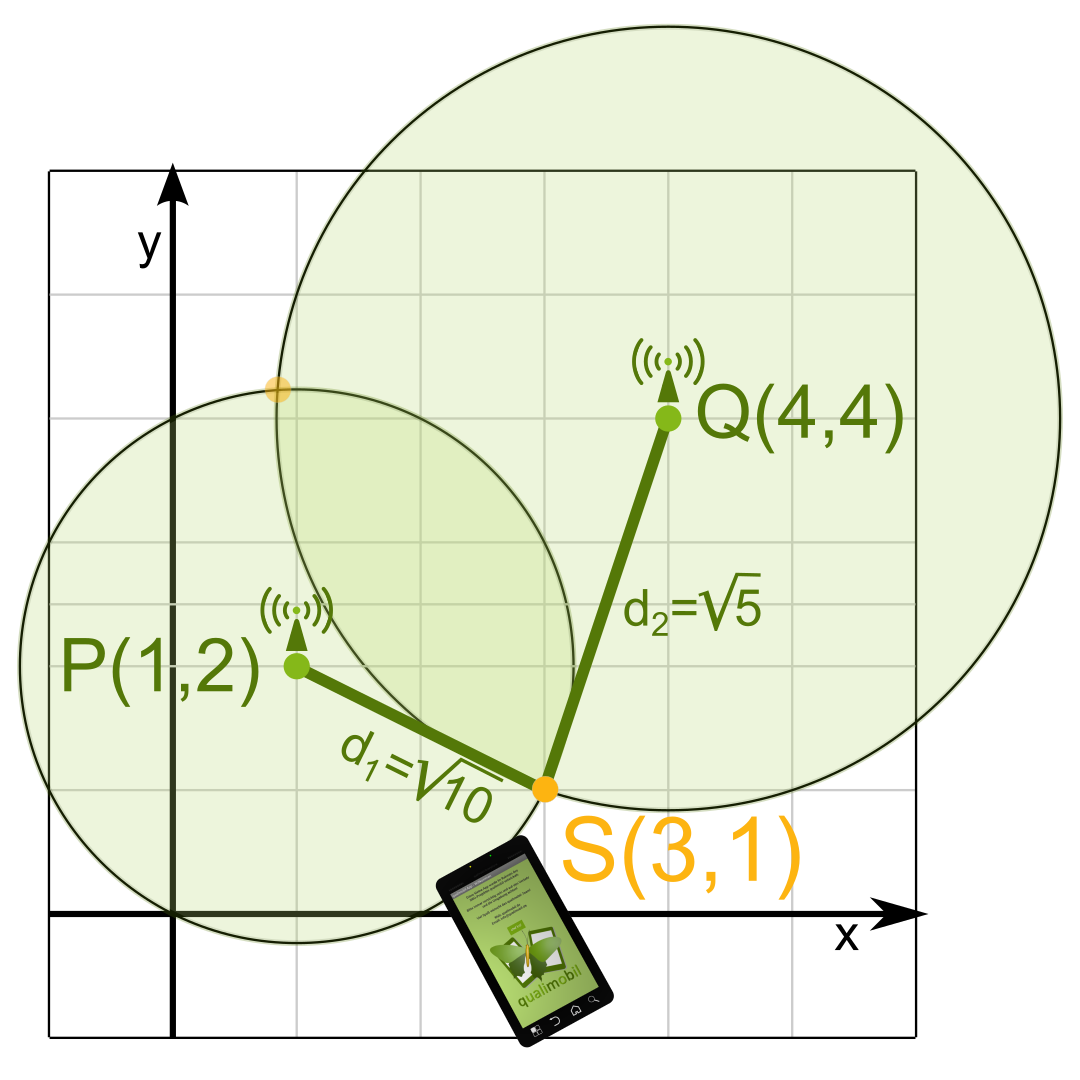
Entfernungsbestimmung zweier Punkte im Raum
Bleiben wir einfach bei dem Beispiel mit den zwei Funkstationen und dem Smartphone.
Gegeben sind also die Fixpunkte {jmimetex} P(1,2){/jmimetex} und {jmimetex} Q(4,4){/jmimetex}
sowie die Entfernungen (Radien)
{jmimetex} {d_1}=\sqrt5{/jmimetex} und {jmimetex} {d_2}=\sqrt10{/jmimetex}
Gesucht werden die Koordinaten des Punktes {jmimetex} S{/jmimetex}.
Ausgangsgleichungen:
{jmimetex}(x_p-x_s)^2+(y_p-y_s)^2={d_1}^2{/jmimetex}
{jmimetex}(x_q-x_s)^2+(y_q-y_s)^2={d_2}^2{/jmimetex}
Werte des Beispiels:
{jmimetex} x_p=1, y_p=2, x_q=4, y_q=4, d_1=\sqrt{5}, d_2=\sqrt{10}{/jmimetex}
Einsetzen der Werte:
{jmimetex}(1-x_s)^2+(2-y_s)^2=5{/jmimetex}
{jmimetex}(4-x_s)^2+(4-y_s)^2=10{/jmimetex}
Anwenden der binomischen Formel:
{jmimetex} 1-2x_s+x_s^2+4-4y_s+y_s^2=5{/jmimetex}
{jmimetex} 16-8x_s+x_s^2+16-8y_s+y_s^2=10{/jmimetex}
Ordnen / Vereinfachen
{jmimetex} x_s^2-2x_s-4y_s+y_s^2=0{/jmimetex} (Gleichung I.)
{jmimetex} x_s^2-8x_s-8y_s+y_s^2=-22{/jmimetex} (Gleichung II.)
Gleichung II. von Gleichung I. abziehen ({jmimetex}{x_s}^2{/jmimetex} und {jmimetex}{y_s}^2{/jmimetex} fallen weg)
{jmimetex} 6x_s+4y_s=22{/jmimetex}
Vereinfachen
{jmimetex} 3x_s+2y_s=11{/jmimetex}
nach {jmimetex}y_s{/jmimetex} auflösen
{jmimetex} y_s=\frac {11-3x_s}{2}{/jmimetex}
{jmimetex} y_s{/jmimetex} in Gleichung I. einsetzen und Normalform herstellen ({jmimetex} a x^2 +b x + c =0{/jmimetex})
{jmimetex} x_s^2-2x_s-4y_s+y_s^2=0{/jmimetex} (Gleichung I.)
{jmimetex} x_s^2-2x_s-4(\frac {11-3x_s}{2})+(\frac {11-3x_s}{2})^2=0{/jmimetex}
{jmimetex} x_s^2-2x_s-\frac {44-12x_s}{2}+\frac {(121-66x_s+9x_s^2)}{4}=0{/jmimetex}
{jmimetex} 4x_s^2-8x_s-88+24x_s+121-66x_s+9x_s^2=0{/jmimetex}
{jmimetex} 13x_s^2-50x_s+33=0{/jmimetex}
Lösungsformel anwenden
{jmimetex} x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}{/jmimetex}
{jmimetex} x_{1,2}=\frac{-(-50)\pm\sqrt{(-50)^2-4\cdot13\cdot33}}{2\cdot13}{/jmimetex}
{jmimetex} x_{1,2}=\frac{50\pm\sqrt{2500-1716}}{26}{/jmimetex}
{jmimetex} x_{1,2}=\frac{50\pm\sqrt{784}}{26}{/jmimetex}
{jmimetex} x_{1,2}=\frac{50\pm28}{26}{/jmimetex}
{jmimetex} x_1=3{/jmimetex}
{jmimetex} x_2=\approx 0,846...{/jmimetex}
Einsetzen in {jmimetex} y_s=\frac {11-3x_s}{2}{/jmimetex}
{jmimetex} y_1=1{/jmimetex}
{jmimetex} y_2=\approx 4,230...{/jmimetex}
Lösung
Der gesuchte Schnittpunkt {jmimetex}S{/jmimetex} besitzt die Koordinaten {jmimetex}(3,1){/jmimetex},
der zweite Schnittpunkt -die zweite mögliche Position, die aufgrund bestimmter Bedingungen auf die hier nicht weiter eingegangen wird ausgeschlossen werden kann- liegt bei {jmimetex}(0,846...,4,230...){/jmimetex}.