Entfernungsbestimmung zweier Punkte in der Ebene
Zur Berechnung der Entfernung zweier Punkte in einem zweidimensionalen kartesischen Koordinatensystem, soll das folgende Beispiel dienen.
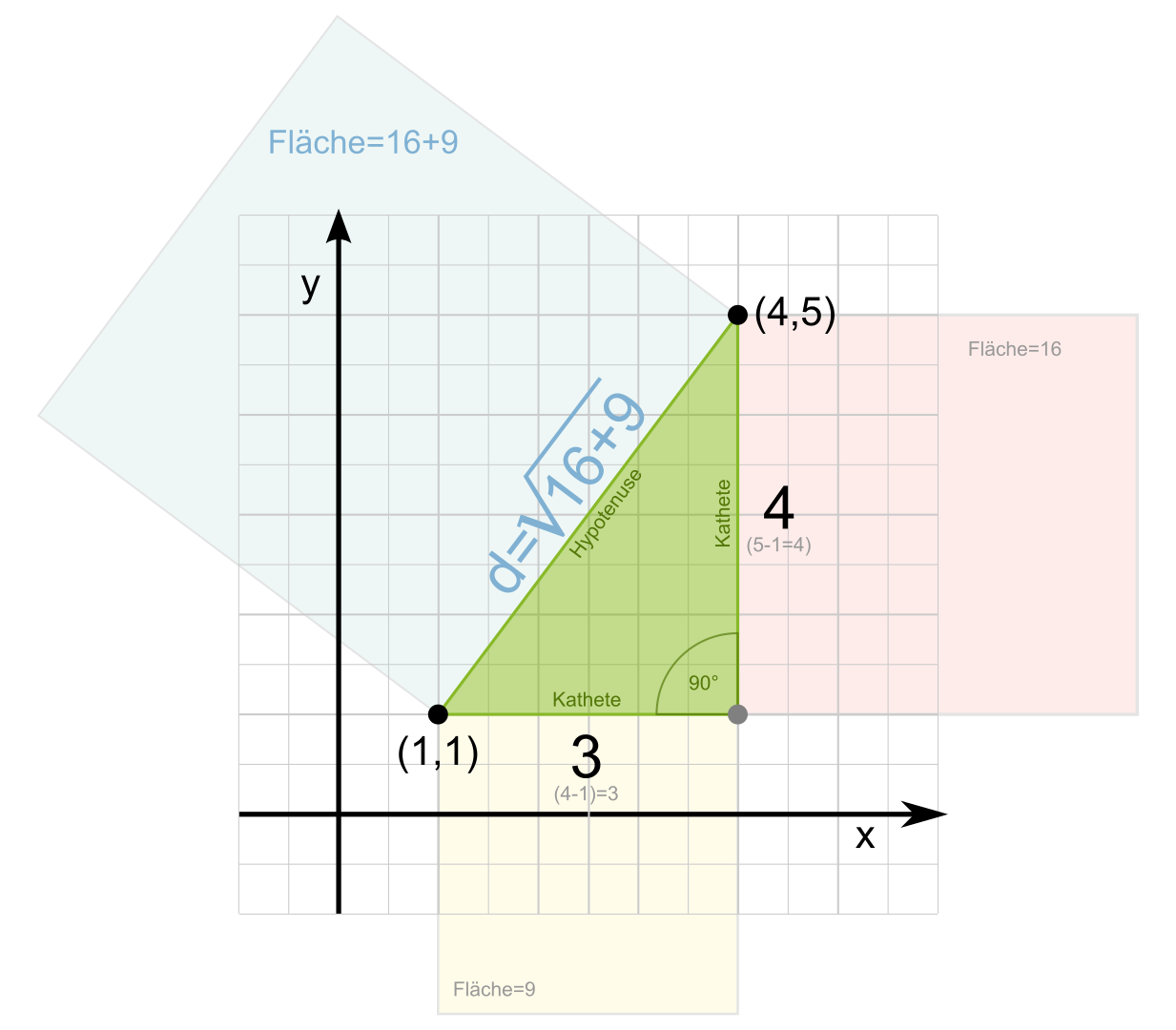
Gegeben sind die beiden Punkte {jmimetex}P(4,5){/jmimetex} und {jmimetex}Q(1,1){/jmimetex}.
Schritt 1: Wir konstruieren ein rechtwinkliges Dreieck.
Die Hypotenuse ist vorgegeben als die Seite, die {jmimetex}P{/jmimetex} und {jmimetex}Q{/jmimetex} verbindet. Die Seiten {jmimetex}a{/jmimetex} und {jmimetex}b{/jmimetex} verlaufen parallel zu jeweils einer Achse des Koordinatensystem, sodass die Seiten (zwangsläufig) in einem rechten Winkel aufeinandertreffen. Der Schnittpunkt liegt jetzt auf einer Geraden, die durch den Punkt {jmimetex}P{/jmimetex} verläuft und gleichzeitig auf einer Geraden, die durch die Punkt {jmimetex}Q{/jmimetex} verläuft. Dadurch ergeben sich jetzt in einfacher Weise die Längen der Katheten durch {jmimetex}P(x)-Q(x){/jmimetex} und {jmimetex}P(y)-Q(y){/jmimetex}, also 4-1=3 und 5-1=4.
Schritt 2: Wir berechnen die Entfernung.
Wir haben also die Seitenlängen der Katheten. Um jetzt zum Satz des Pythagoras zugehörige Formel anzuwenden, lösen wir diese nach {jmimetex}c{/jmimetex} (Länge der Hypotenuse) auf.
{jmimetex}a^2 = b^2 + c^2{/jmimetex}
{jmimetex}c = \sqrt{a^2 + b^2}{/jmimetex}
Wird {jmimetex}c{/jmimetex} umbenannt in {jmimetex}d{/jmimetex} (Distanz) und {jmimetex}a{/jmimetex} und {jmimetex}b{/jmimetex} werden durch die Differenzen der jeweiligen {jmimetex}x{/jmimetex} - und {jmimetex}y{/jmimetex}-Werte unserer Punkte ersetzt, dann ergibt sich die folgende Formel:
{jmimetex}d = \sqrt{(P_x - Q_x)^2 + (P_y - Q_y)^2}{/jmimetex}
Jetzt müssen nur noch die Werte in die Gleichung eingesetzt werden. Für die Entfernung der beiden Punkte P und Q, die in einem kartesischen Koordinatensystem auch euklidischer Abstand genannt wird, ergibt sich schließlich für unser Beispiel der Wert 5.
{jmimetex}d = \sqrt{(4 - 1)^2 + (5 - 1)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5{/jmimetex}
Nun weißt Du wie der Abstand zweier Punkte in der Ebene berechnet werden kann.
Jetzt folgt der dreidimensionale Fall, der ähnlich ist.