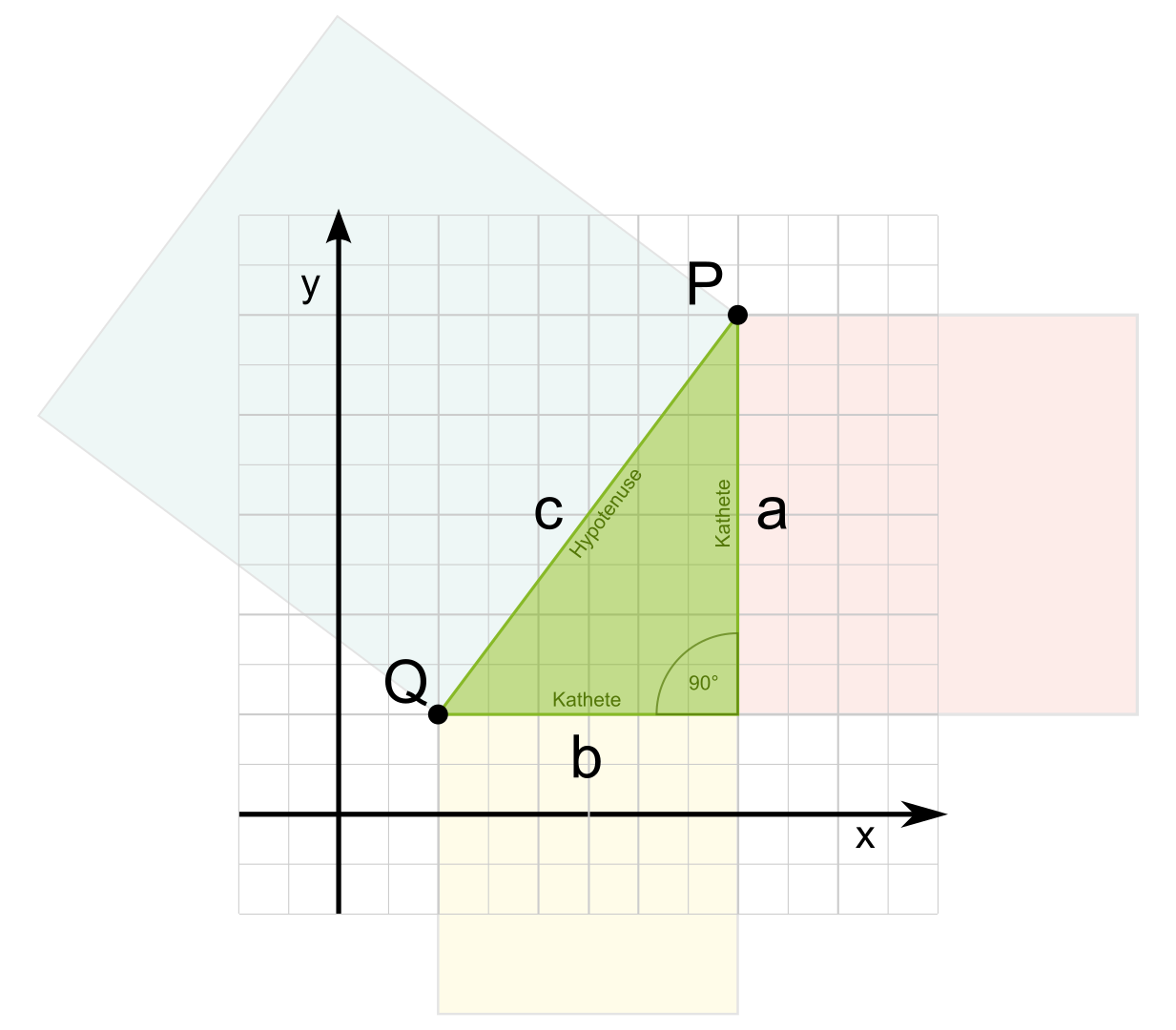
Bei der Berechnung der Entfernung zwischen zwei Punkten in einem zwei- oder dreidimensionalen kartesischen Koordinatensystem, kann in einfacher Weise ein rechtwinkliges Dreieck konstruiert werden, auf das der Satz des Pythagoras angewendet werden kann.
In einem rechtwinkligen Dreieck ist die Summe der Flächen der Kathetenquadrate gleich der Fläche des Hypotenusenquadrates.
Der Satz als Formel ausgedrückt lautet: {jmimetex}\Large a^2+b^2=c^2{/jmimetex}
Wie Du in der Abbildung sehen kannst, entspricht die Entfernung zwischen den Punkten {jmimetex}P{/jmimetex} und {jmimetex}Q{/jmimetex} der Länge der Hypotenuse bzw. der Seite {jmimetex}c{/jmimetex} bzw. der Seitenlänge des Hypotenusenquadrates.
Da {jmimetex}a{/jmimetex}, {jmimetex}b{/jmimetex} u. {jmimetex}c{/jmimetex} in der Formel die Seitenlängen des Dreiecks repräsentieren, lässt sich {jmimetex}c{/jmimetex} berechnen, wenn {jmimetex}a{/jmimetex} und {jmimetex}b{/jmimetex} bekannt sind.
Darauf läuft das nun folgende Beispiel hinaus.