Inhaltsvorschau

Ein beliebiger Punkt auf der Erdoberfläche wird häufig in einem Geographischen Koordinatensystem durch die Geographische Länge λ (Lambda) und Geographische Breite φ (Phi) angegeben.

Die Geographsche Breite ist der Winkel, den eine gedachte Linie durch einen Punkt auf der Erdoberfläche und den Erdmittelpunkt mit der Äquatorebene bildet. Der Äquator ist der senkrecht zur Erdachse stehende Kreis, dessen Ebene durch den Erdmittelpunkt geht. Die parallel zum Äquator verlaufenden Kreise sind die sog. Breitenkreise.

Die Geographische Länge ist der Winkel zwischen der Meridianebene eines Punktes auf der Erdoberfläche und der Nullmeridianebene. Die Meridiane oder Längenkreise sind die durch die Pole verlaufenden und vertikal zum Äquator (und zu den Breitenkreisen) stehenden Kreise. Als Nullmeridian wurde 1884 der durch die Sternwarte Greenwich bei London verlaufende Längenkreis vereinbart.

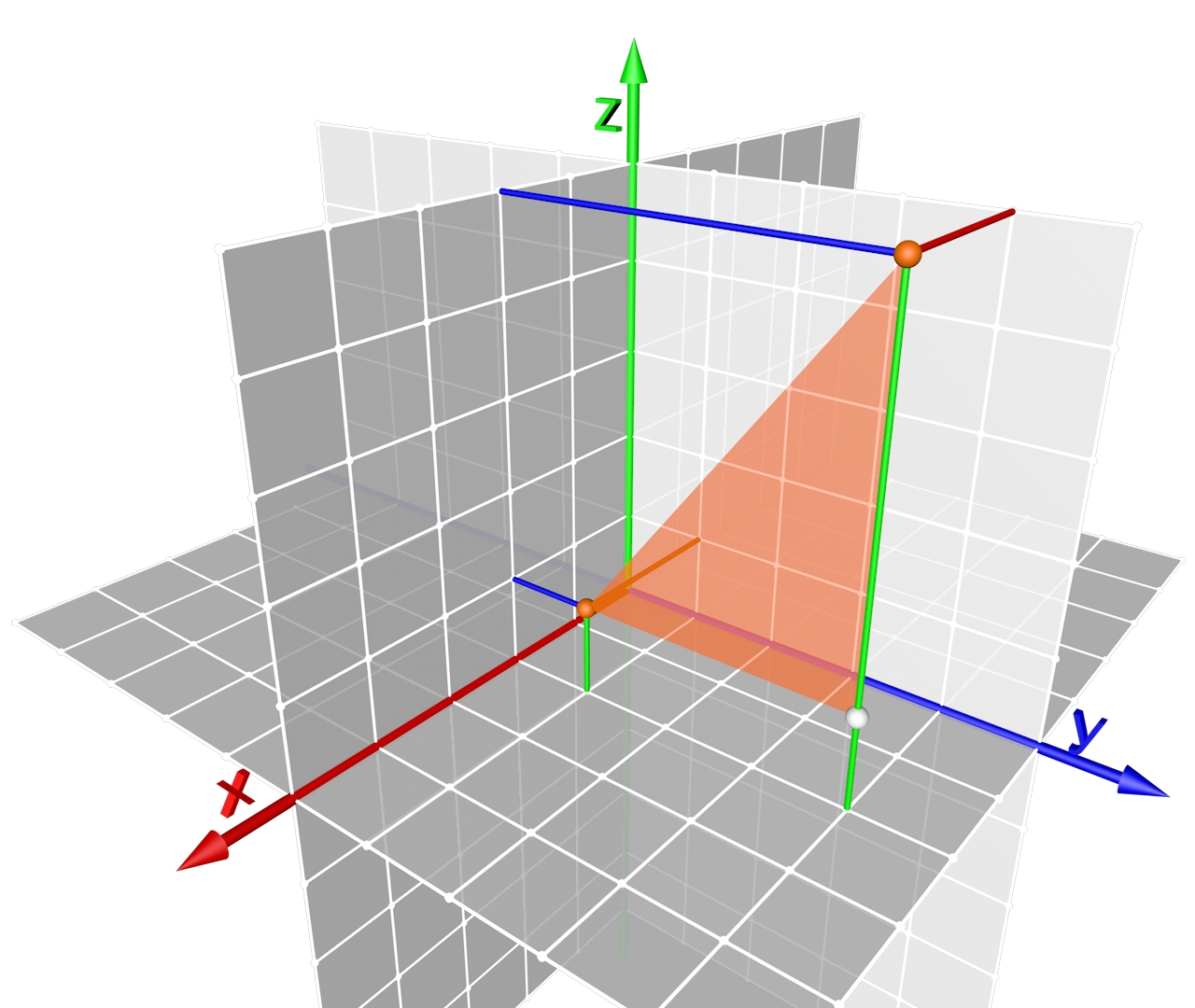
Die Abbildung zeigt die Position der Cheops-Pyramide Cheops-Pyramide 29.979150° Nord 31.134244° Ost.
In diesen Fall bedeutet "Nord", dass der Winkel vom Äquator ausgehend in nördlicher Richtung erzeugt wird und "Ost", dass der Winkel vom Nullmeridian aus in östlicher Richtung erzeugt wird. Die Die rote Fläche repräsentiert somit die Geographische Länge, die blaue Fläche die Geographische Breite.

 
Nun weißt Du wie Positionen eindeutig auf der Erdoberfläche verortet werden können.
Wie diese Positionen berechnet werden soll jetzt Thema sein.

Entfernungsbestimmung zweier Punkte in der Ebene

Zur Berechnung der Entfernung zweier Punkte in einem zweidimensionalen kartesischen Koordinatensystem, soll das folgende Beispiel dienen.

Gegeben sind die beiden Punkte {jmimetex}P(4,5){/jmimetex} und {jmimetex}Q(1,1){/jmimetex}.

Schritt 1: Wir konstruieren ein rechtwinkliges Dreieck.
Die Hypotenuse ist vorgegeben als die Seite, die {jmimetex}P{/jmimetex} und {jmimetex}Q{/jmimetex} verbindet. Die Seiten {jmimetex}a{/jmimetex} und {jmimetex}b{/jmimetex} verlaufen parallel zu jeweils einer Achse des Koordinatensystem, sodass die Seiten (zwangsläufig) in einem rechten Winkel aufeinandertreffen. Der Schnittpunkt liegt jetzt auf einer Geraden, die durch den Punkt {jmimetex}P{/jmimetex} verläuft und gleichzeitig auf einer Geraden, die durch die Punkt {jmimetex}Q{/jmimetex} verläuft. Dadurch ergeben sich jetzt in einfacher Weise die Längen der Katheten durch {jmimetex}P(x)-Q(x){/jmimetex} und {jmimetex}P(y)-Q(y){/jmimetex}, also 4-1=3 und 5-1=4.

Schritt 2: Wir berechnen die Entfernung.
Wir haben also die Seitenlängen der Katheten. Um jetzt zum Satz des Pythagoras zugehörige Formel anzuwenden, lösen wir diese nach {jmimetex}c{/jmimetex} (Länge der Hypotenuse) auf.

{jmimetex}a^2 = b^2 + c^2{/jmimetex}

{jmimetex}c = \sqrt{a^2 + b^2}{/jmimetex}

Wird {jmimetex}c{/jmimetex} umbenannt in {jmimetex}d{/jmimetex} (Distanz) und {jmimetex}a{/jmimetex} und {jmimetex}b{/jmimetex} werden durch die Differenzen der jeweiligen {jmimetex}x{/jmimetex} - und {jmimetex}y{/jmimetex}-Werte unserer Punkte ersetzt, dann ergibt sich die folgende Formel:

Jetzt müssen nur noch die Werte in die Gleichung eingesetzt werden. Für die Entfernung der beiden Punkte P und Q, die in einem kartesischen Koordinatensystem auch euklidischer Abstand  genannt wird, ergibt sich schließlich für unser Beispiel der Wert 5.

 
Nun weißt Du wie der Abstand zweier Punkte in der Ebene berechnet werden kann.
Jetzt folgt der dreidimensionale Fall, der ähnlich ist.

Bei der Berechnung der Entfernung zwischen zwei Punkten in einem zwei- oder dreidimensionalen kartesischen Koordinatensystem, kann in einfacher Weise ein rechtwinkliges Dreieck konstruiert werden, auf das der Satz des Pythagoras angewendet werden kann.

Der Satz als Formel ausgedrückt lautet: {jmimetex}\Large a^2+b^2=c^2{/jmimetex}

Wie Du in der Abbildung sehen kannst, entspricht die Entfernung zwischen den Punkten {jmimetex}P{/jmimetex} und {jmimetex}Q{/jmimetex} der Länge der Hypotenuse bzw. der Seite {jmimetex}c{/jmimetex} bzw. der Seitenlänge des Hypotenusenquadrates.

Da {jmimetex}a{/jmimetex}, {jmimetex}b{/jmimetex} u. {jmimetex}c{/jmimetex} in der Formel die Seitenlängen des Dreiecks repräsentieren, lässt sich {jmimetex}c{/jmimetex} berechnen, wenn {jmimetex}a{/jmimetex} und {jmimetex}b{/jmimetex} bekannt sind.

Darauf läuft das nun folgende Beispiel hinaus.

Entfernungsbestimmung zweier Punkte im Raum

Zur Berechnung der Entfernung zweier Punkte in einem dreidimensionalen kartesischen Koordinatensystem soll unser Dreieck aus dem vorangegangenem Beispiel dienen.
Dieses ist jetzt in einem dreidiemensionalen kartesischen Koordinatensystem aufgestellt, wie die Abbildung zeigt.

Die Hypothenuse ist die zu ermittelnde Entfernung der beiden Punkte {jmimetex}P (2,1,1){/jmimetex} (untere orange Kugel) und {jmimetex}Q (2,4,5){/jmimetex} (obere orange Kugel) unseres rechtwinkligen Dreiecks.

Die Formel zur Berechnung wird jetzt erweitert und dabei berücksichtigt, dass die Punkte jetzt über Koordinatentripel definiert sind.

Jetzt werden wieder die Werte in die Gleichung eingesetzt.

Hinweis:
Zur einfacheren Darstellung besaßen die rechtwinklingen Dreiecke der Beispiele die Kathetenlängen 3 und 4 und die damit einhergehende Hypthenusenlänge von 5 als Sonderfall.
Im dreidimensionalen Fall müssen die Punkte des Dreiecks zudem nicht in einer Ebene liegen.

Langsam nähern wir uns der Berechnung einer GPS-Position, dazu soll jetzt zunächst gezeigt werden, wie eine Position in der Ebene bestimmt werden kann, wenn zwei bekannte Fixpunkte  gegeben sind.