Allgemeiner Fall
Die Position eines Punktes {jmimetex}S{/jmimetex} in einer Ebene lässt sich ebenfalls bestimmen, wenn die Koordinaten zweier Fixpunkte {jmimetex}P{/jmimetex} und {jmimetex}Q{/jmimetex} und wenn ebenfalls die beiden Entfernungen von {jmimetex}S{/jmimetex} zu den beiden Fixpunkten bekannt sind.
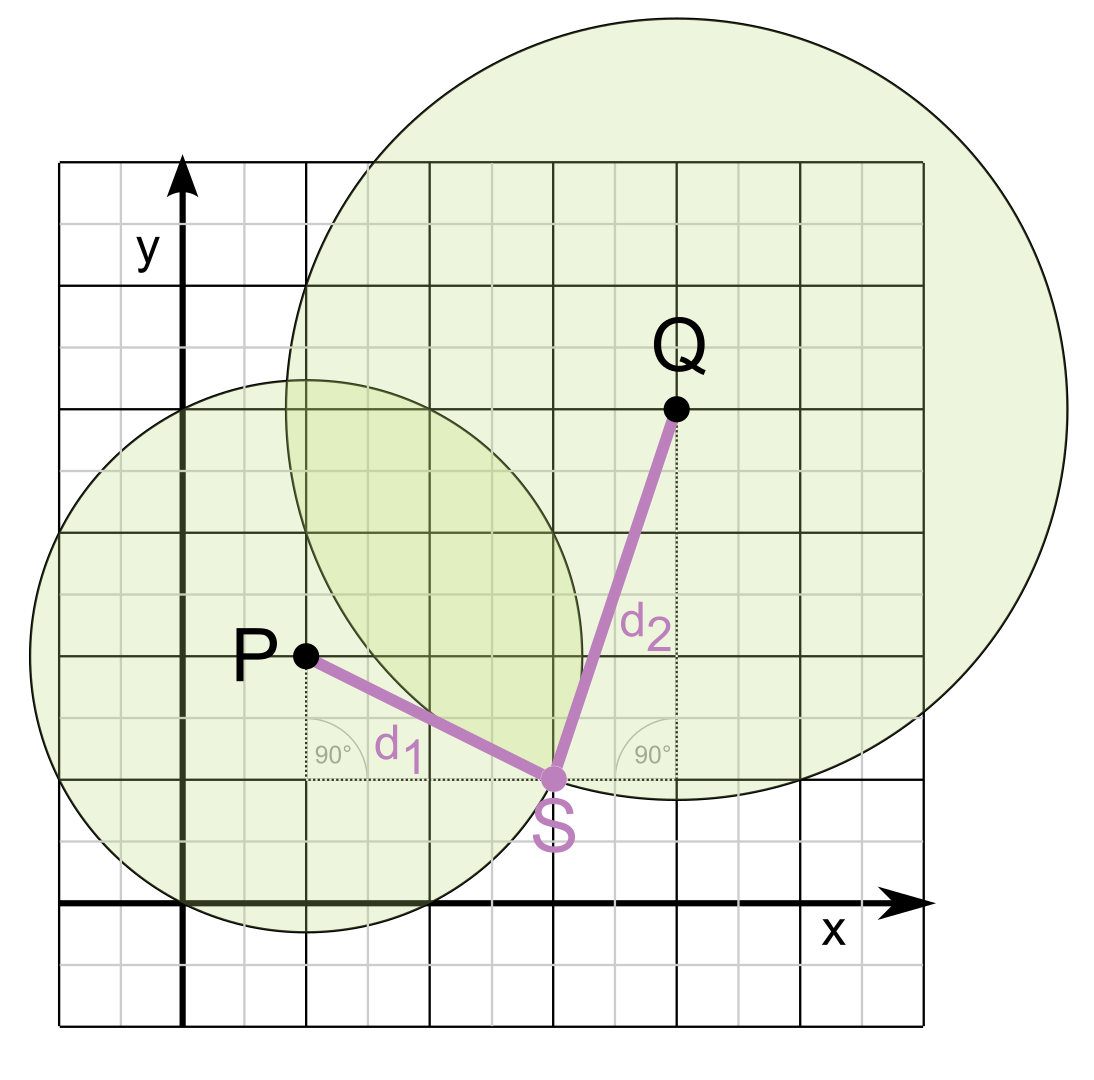
Positionsbestimmung mittels zweier Fixpunkte
Die Abbildung zeigt den allgemeinen Fall. Nach den nun bekannten Formeln zur Berechnung von Abständen zwischen zwei Punkten lassen sich zwei Bestimmungsgleichungen aufstellen mit den beiden unbekannten Werten für die {jmimetex}x{/jmimetex}- und {jmimetex}y{/jmimetex}-Koordinate des Standortes S.
Dieses Gleichungssystem kann mit Methoden der Algebra nach den Koordinaten {jmimetex}x_s{/jmimetex} und {jmimetex}y_s{/jmimetex} des gesuchten Standortes aufgelöst werden.
Aus der Darstellung ergibt sich auch eine einfache geometrische Konstruktionsvorschrift zur Bestimmung des unbekannten Standortes {jmimetex}S{/jmimetex}. Um die beiden Fixpunkte {jmimetex}P{/jmimetex} und {jmimetex}Q{/jmimetex} werden Kreise mit dem Radius der Entfernungen {jmimetex}\overline{P S}{/jmimetex} und {jmimetex}\overline{Q S}{/jmimetex} geschlagen. Die beiden Kreise schneiden sich in zwei Punkten, von denen einer in der Regel sofort ausgeschlossen werden kann. Der Sonderfall nur eines einzigen Berührpunktes wurde hier nicht weiter betrachtet.
Exkurs:
Die Positionsbestimmung mittels Fixpunkten hat unabhängig von GPS bereits einen direkten Anwendungsbezug. Als Stichwort sei "Indoor Positioning" genannt.
Die Positionsbestimmung innerhalb von Gebäuden ist natürlich auch für mobile ortsbezogene Lernangebote interessant, spätestens dann, wenn kein GPS-Signal vorhanden ist bzw. genutzt werden kann, wie in einem Glashaus eines Botanischen Gartens oder in einem unterirdischen Zoo.
Stelle dir den folgenden vereinfachten Anwendungsfall vor:
Zwei Stationen senden ein Funksignal mit gleicher Ausbreitungsgeschwindigkeit, das von deinem Smartphone empfangen wird. Über eine Laufzeitmessung des Signals ermittelt dein Smartphone die Entfernungen zu den Stationen. Sind die Standorte der Stationen bekannt sind, dann kannst Du den eigenen Standort berechnen.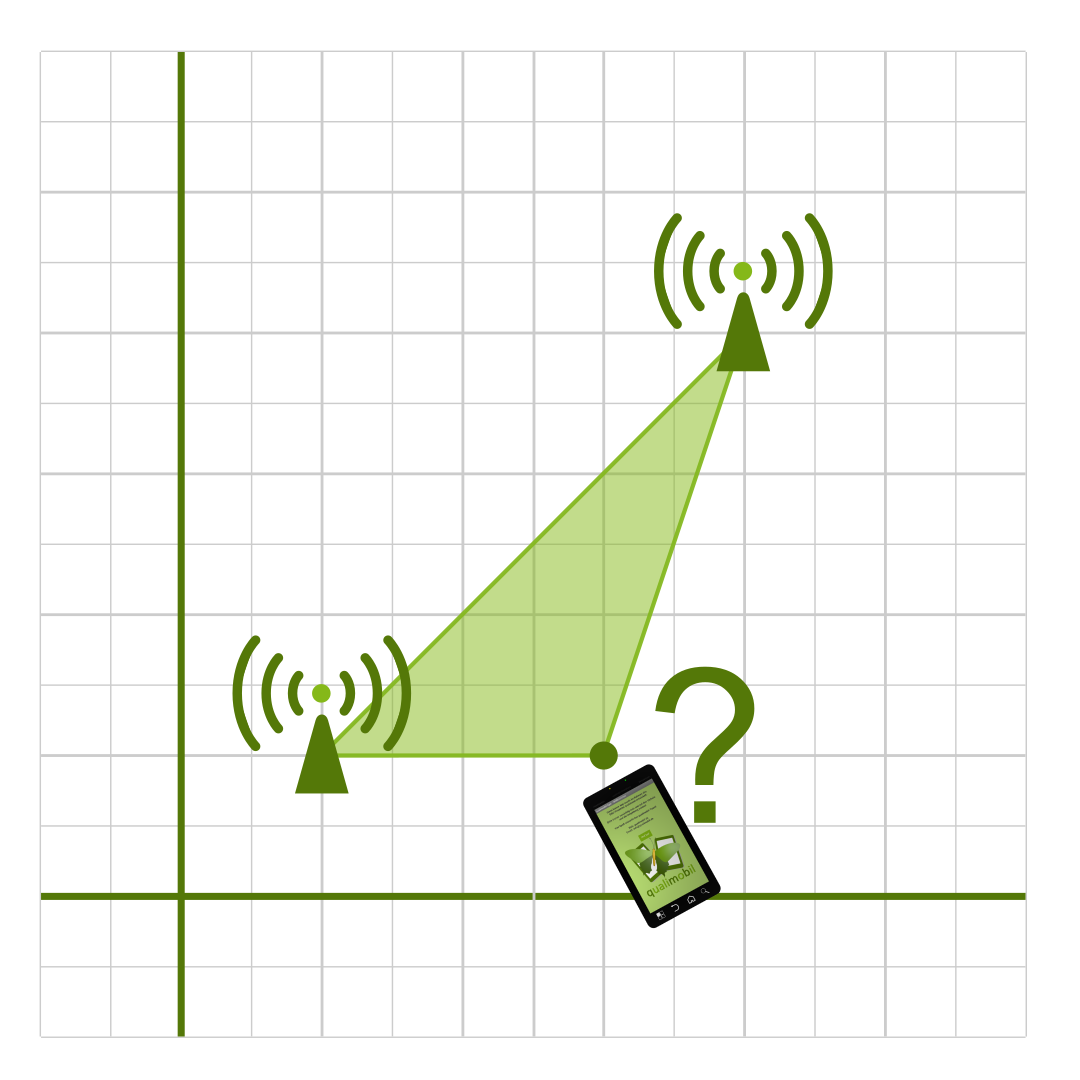
Die Bestimmung einer GPS-Position geschieht ebenfalls mithilfe von bekannten Fixpunkten, nämlich denen der Satelliten, die ihre Positionen per Funk senden.
Vielleicht kannst Du dir schon vorstellen, wie das ganze funktioniert.
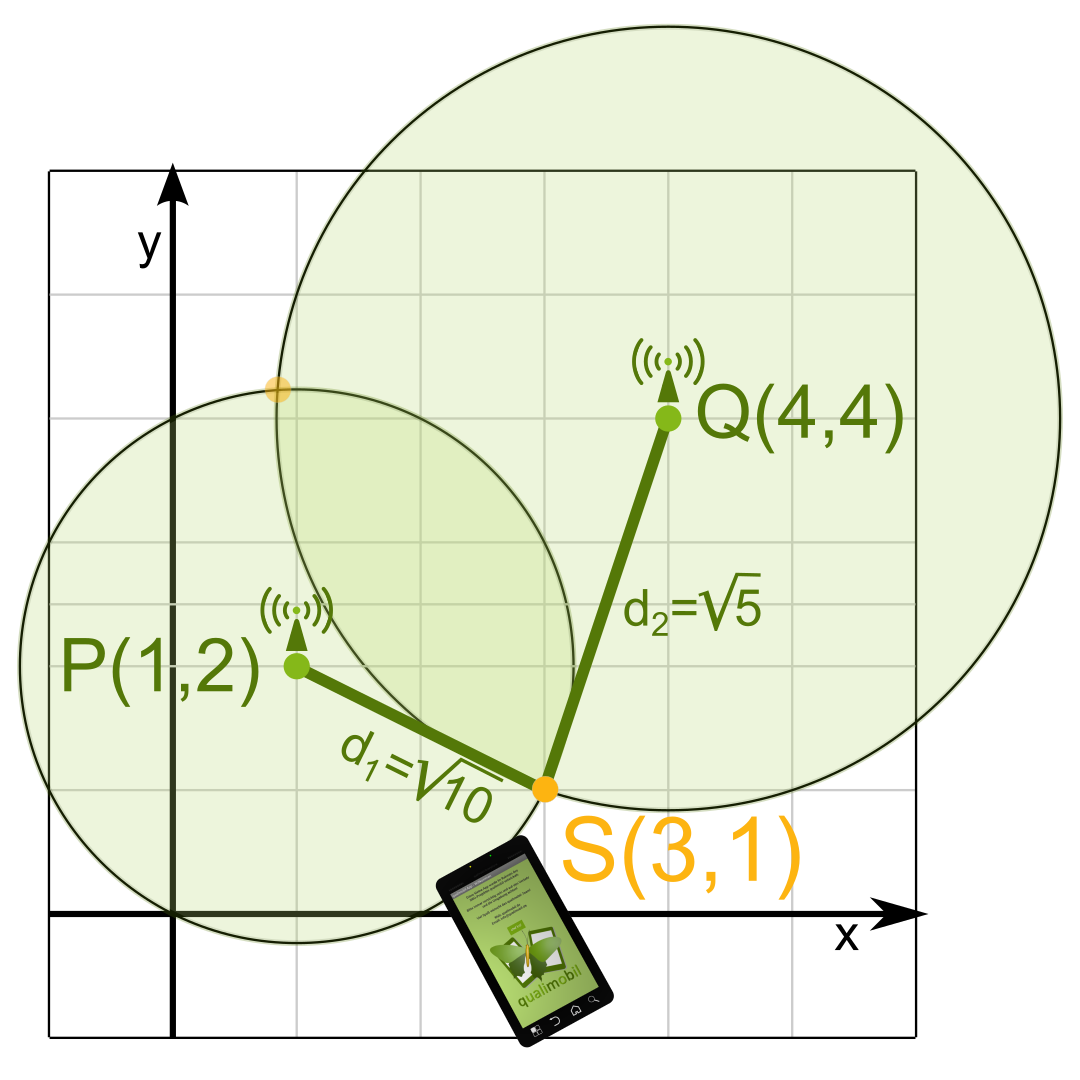
Da die Berechnung der Position bei gegebenen zwei Fixpunkten nicht ganz so einfach ist, wie die Berechnung der Entfernung zweier Punkte in der Ebene, soll zuvor noch ein konkretes Rechenbeispiel gegeben werden.